Home
Power of a Power Property of Exponents
Adding and Subtracting Rational Numbers
Point
Solving Equations with Radicals and Exponents
Quadratic Equations
Using Intercepts for Graphing Linear Equations
Graphing Linear Equations in Two
Exponents
Multiplying Fractions
Solving Linear Equations Containing Fractions
Evaluating Polynomials
Multiplication Property of Square and Cube Roots
Writing a Fraction in Simplest Form
Square Roots
Inequalities
The Pythagorean Theorem
Factoring The Difference of 2 Squares
Solving Polynomial Equations
Roots and Powers
Writing Linear Equations in Standard Form
Solving Nonlinear Equations by Substitution
Straight Lines
The Square of a Binomial
Solving Equations
Adding and Subtracting Like Fractions
Point
Finding the Equation of an Inverse Function
Slope of a Line
Rules for Nonnegative Integral Exponents

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Squaring a Sum

To find (a + b)², the square of a sum, we can use FOIL on (a + b)(a + b):

(a + b)(a + b)	= a² + ab + ab + b²
	= a² + 2ab + b²

You can use the result a² + 2ab + b² that we obtained from FOIL to quickly find the square of any sum. To square a sum, we square the first term (a²), add twice the product of the two terms (2ab), then add the square of the last term (b²).

Rule for the Square of a Sum

(a + b)² = a² + 2ab + b²

In general, the square of a sum (a + b)²is not equal to the sum of the squares a² + b². The square of a sum has the middle term 2ab.

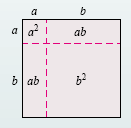
Helpful hint

To visualize the square of a sum, draw a square with sides of length a + b as shown.

The area of the large square is (a + b)². It comes from four terms as stated in the rule for the square of a sum.

Example 2

Squaring a sum

Square each sum, using the new rule.

a) (x + 5)²

b) (2w + 3)²

c) (2y⁴ + 3)²

Solution

a) (x + 5)²	= x² +	2(x)(5)	+ 5²	= x² + 10x + 25
	↑ Square of first	↑ Twice the product	↑ Square of last

b) (2w + 3)² = (2w)² + 2(2w)(3) + 3² = 4w² + 12w + 9

c) (2y⁴ + 3)² = (2y⁴)² + 2(2y⁴)(3) + 3² = 4y⁸ + 12y⁴ + 9

Caution

Squaring x + 5 correctly, as in Example 2(a), gives us the identity (x + 5)² = x² + 10x + 25, which is satisfied by any x. If you forget the middle term and write (x + 5)² = x² + 25, then you have an equation that is satisfied only if x = 0.

Helpful hint

You can use

(x + 5)²	= x² + 10x + 25
	= x(x + 10) + 25

to learn a trick for squaring a number that ends in 5. For example, to find 25², find 20 Â· 30 + 25 or 625. More simply, to find 35², find 3 Â· 4 = 12 and follow that by 25: 35² = 1225.