Finding the Equation of an Inverse Function
Example
Given
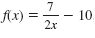 ,
find f-1(x). ,
find f-1(x).
Solution
| Step 1 |
Replace f(x) with y.
|
y |
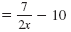 |
| Step 2 |
Switch the variables y and x.
|
x |
 |
| Step 3 |
Solve for y. |
|
|
| |
Multiply each side by the LCD, 2y. |
2y · x |
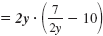 |
| |
Simplify. Add 20y to both sides.
Factor out y. |
2xy 2xy + 20y
y(2x + 20) |
= 7 - 20y = 7
= 7 |
| |
Divide both sides by 2x + 20. |
y |
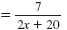 |
| Step 4 |
Replace y with f -1(x). |
f-1(x) |
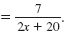 |
So, the inverse of
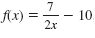 is f-1(x) is f-1(x)
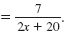
Note:
Here is another way to solve
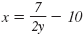 for y: for y:
| Add 10 to both sides. |
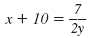 |
| Multiply by the LCD, 2y. |
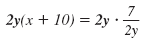 |
| Simplify on the right. |
2y(x + 10) = 7 |
| Divide both sides by 2(x + 10). |
 |
|