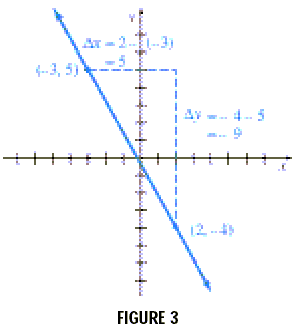
Slope of a Line

An important characteristic of a straight line is its slope, a number that represents the “steepness” of the line. To see how slope is defined, look at the line in Figure 3. The line goes through the points (x₁, y₁) = (-3, 5) and (x₂, y₂) = (2, -4).

The difference in the two x -values,

x₂ - x₁ = 2 - (-3) = 5

in this example, is called the change in x. The symbol (read “delta x” ) is used to represent the change in x . In the same way, represents the change in y. In our example,

y = y₂ - y₁

= - 4 - 5

= -9

These symbols, x and y, are used in the following definition of slope.

Slope of a Line

The slope of a line is defined as the vertical change (the “rise” ) over the horizontal change (the “run” ) as one travels along the line. In symbols, taking two different points (x₁, y₁) and (x₂, y₂) on the line, the slope is

where x₁ x₂.

By this definition, the slope of the line in Figure 3 is

The slope of a line tells how fast y changes for each unit of change in x.

NOTE Using similar triangles, it can be shown that the slope of a line is independent of the choice of points on the line. That is, the same slope will be obtained for any choice of two different points on the line.

Example 1

Slope

Find the slope through each of the following pairs of points.

(a) (-7, 6) and (4, 5)

Solution

Let (x₁, y₁) = (-7, 6) and (x₂, y₂) = (4, 5). Use the definition of slope.

(b) (5, -3) and (-2, -3)

Solution

Let and (x₁, y₁) = (5, -3) and (x₂, y₂) = (-2, -3). Then

Lines with zero slope are horizontal (parallel to the x-axis).

(c) (2, -4) and (2, 3)

Solution

Let (x₁, y₁) = (2, -4) and (x₂, y₂) = (2, 3). Then

which is undefined. This happens when the line is vertical (parallel to the y-axis).

CAUTION The phrase “no slope” should be avoided; specify instead whether the slope is zero or undefined.

In finding the slope of the line in Example 1(a) we could have let (x₁, y₁) = (4, 5) and (x₂, y₂) = (-7, 6). In that case,

the same answer as before. The order in which coordinates are subtracted does not matter, as long as it is done consistently.

Figure 4 shows examples of lines with different slopes. Lines with positive slopes go up from left to right, while lines with negative slopes go down from left to right.

It might help you to compare slope with the percent grade of a hill. If a sign says a hill has a 10% grade uphill, this means the slope is .10, or so the hill rises 1 foot for every 10 feet horizontally. A 15% grade downhill means the slope is -.15.