Home
Power of a Power Property of Exponents
Adding and Subtracting Rational Numbers
Point
Solving Equations with Radicals and Exponents
Quadratic Equations
Using Intercepts for Graphing Linear Equations
Graphing Linear Equations in Two
Exponents
Multiplying Fractions
Solving Linear Equations Containing Fractions
Evaluating Polynomials
Multiplication Property of Square and Cube Roots
Writing a Fraction in Simplest Form
Square Roots
Inequalities
The Pythagorean Theorem
Factoring The Difference of 2 Squares
Solving Polynomial Equations
Roots and Powers
Writing Linear Equations in Standard Form
Solving Nonlinear Equations by Substitution
Straight Lines
The Square of a Binomial
Solving Equations
Adding and Subtracting Like Fractions
Point
Finding the Equation of an Inverse Function
Slope of a Line
Rules for Nonnegative Integral Exponents

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Using Intercepts for Graphing Linear Equations

The x-intercept of a line is the point where the line crosses the x-axis. The x-intercept has a y-coordinate of 0. Similarly, the y-intercept of a line is the point where the line crosses the y-axis. The y-intercept has an x-coordinate of 0. If a line has distinct x- and y-intercepts, then these intercepts can be used as two points that determine the location of the line. (Horizontal lines, vertical lines, and lines through the origin do not have two distinct intercepts.)

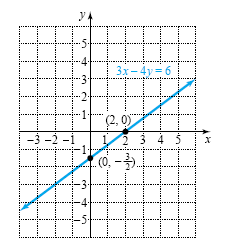
Example 1

Using intercepts to graph

Use the intercepts to graph the line 3x - 4y = 6.

Solution

Let x = 0 in 3x - 4y = 6 to find the y-intercept:

3(0) - 4y	= 6
-4y	= 6
y

Let y = 0 in 3x - 4y = 6 to find the x-intercept:

3x - 4(0)	= 6
3x	= 6
x	= 2

The y-intercept is, and the x-intercept is (2, 0). The line through the intercepts is shown in the figure below. To check, find another point that satisfies the equation. The point (-2, -3) satisfies the equation and is on the line in the figure below.

Caution

Even though two points determine the location of a line, finding at least three points will help you to avoid errors.