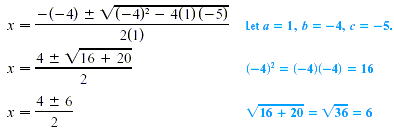Quadratic Equations

An equation with 2 as the highest exponent of the variableis a quadratic equation. A quadratic equation has the form ax + bx + c = 0, where a, b, and c are real numbers and a0. A quadratic equation written in theform is said to be in standard form.

The simplest way to solve a quadratic equation, but one that is not always applicable, is by factoring. This method depends on the zero-factor property.

ZERO-FACTOR PROPERTY

If a and b are real numbers, with ab = 0 then a = 0, b = 0 or both.

Solving Quadratic Equations

EXAMPLE

Solve 6r + 7r - 3.

Solution

First write the equation in standard form.

6r + 7r - 3 = 0

Now factor 6r + 7r - 3 to get

(3r - 1)(2r + 3) = 0

By the zero-factor property, the product (3r - 1)(2r + 3) can equal 0 if and only if

3r - 1 = 0 or 2r + 3 = 0

Solve each of these equations separately to find that the solutions are 1/3 and -3/2. Check these solutions by substituting them in the original equation.

CAUTION

Remember, the zero-factor property requires that the product oftwo (or more) factors be equal to zero, not some other quantity. It would beincorrect to use the zero-factor property with an equation in the form (x + 3)(x - 1) = 4 for example.

If a quadratic equation cannot be solved easily by factoring, use the quadratic formula. (The derivation of the quadratic formula is given in most algebra books.)

QUADRATIC FORMULA

The solutions of the quadratic equation ax + bx + c = 0, where a0, are given by

EXAMPLE

Solve x - 4x - 5 = 0 by the quadratic formula.

Solution

The equation is already in standard form (it has 0 alone on one side of the equals sign), so the values of a, b, and c from the quadratic formula are easily identified. The coefficient of the squared term gives the value of a; here a = -1. Also b = -4 and c = -5 (Be careful to use the correct signs.) Substitute thesevalues into the quadratic formula.

The sign represents the two solutions of the equation. To find both of thesolutions, first use + and then use -.

The two solutions are 5 and -1.

CAUTION

Notice in the quadratic formula that the square root is added to orsubtracted from the value of -b before dividing by 2a.

EXAMPLE

Solve x + 1 = 4x

Solution

First, add -4x on both sides of the equals sign in order to get the equationin standard form.

x - 4x + 1 = 0

Now identify the letters a, b, and c. Here a = 1, b = -4, and c = 1. Substitute these numbers into the quadratic formula.

Simplify the solutions by writing Substituting gives

The two solutions are

The exact values of the solutions are The key on a calculator gives decimal approximations of these solutions (to the nearest thousandth):

NOTE Sometimes the quadratic formula will give a result with a negative number under the radical sign, such as . A solution of this type is not a real number. Since this text deals only with real numbers, such solutions cannot be used.

*The symbol means “is approximately equal to”.