Solving Equations
You will generally find the last operation is the first thing to undo. Imagine you are
computing the equation on a calculator. The last operation you would type is likely to be
the first operation to undo. Let’s look at a really big and messy example; try to spot how
we’re working backwards to undo it!
Big Messy Example:
Solve for x: 2(x - 1)2 + 3 = 21
Solution:
| Subtract 3 from both sides: |
2(x - 1)2 + 3 - 3 = 21 - 3 |
| or: |
2(x - 1)2 = 18 |
| Divide both sides by 2: |
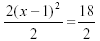 |
| or: |
(x - 1)2 = 9 |
| Square root of both sides: |
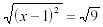 |
| or: |
x - 1 = 3 |
| Finally add 1 to both sides: |
x + 1 - 1 = 3 + 1 |
| or: |
x = 4 |
Check:
Substitute 4 into the original equation:
2•(4-1)2 + 3 = 21
2•32 + 3 = 21
2•9 + 3 = 21
21 = 21 Yes!
|