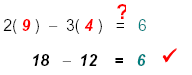Home
Power of a Power Property of Exponents
Adding and Subtracting Rational Numbers
Point
Solving Equations with Radicals and Exponents
Quadratic Equations
Using Intercepts for Graphing Linear Equations
Graphing Linear Equations in Two
Exponents
Multiplying Fractions
Solving Linear Equations Containing Fractions
Evaluating Polynomials
Multiplication Property of Square and Cube Roots
Writing a Fraction in Simplest Form
Square Roots
Inequalities
The Pythagorean Theorem
Factoring The Difference of 2 Squares
Solving Polynomial Equations
Roots and Powers
Writing Linear Equations in Standard Form
Solving Nonlinear Equations by Substitution
Straight Lines
The Square of a Binomial
Solving Equations
Adding and Subtracting Like Fractions
Point
Finding the Equation of an Inverse Function
Slope of a Line
Rules for Nonnegative Integral Exponents

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

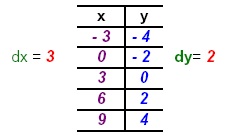
Graphing Linear Equations in Two-Variables

Build a table of ordered pairs where the x-values are in a sequence and the y-values are in a sequence. When you plot these points (ordered pairs) you will see that they form a straight line.

Always choose only an integer as the replacement for the x-value so that the resulting y-value will be an integer, and visa versa. If we put a â€œsequence of integers" in the table for x , complete the computation for each x-value, and put each corresponding y-value in the table, then the y-values in the table will be a â€œsequence of integers". Write the common differences.

1. Given 2x − 3y = 6 build the table for using an arithmetic sequence as replacement values.

Note: In this equation if you choose consecutive integers for x you will find some y-values that are fractions. By noting that the constant 6 is a multiple of 3 and the coefficient of y is 3, you can choose your sequence for the x-values to be multiples of 3 . Now, when you are solving for the y-values and divide by the coefficient-3 you will obtain a sequence of integers for the y-values.

2x − 3y = 6

Let y = - 4: 2x − 3(- 4) = 6, x = - 3

repeat for the other numbers

Check to see that both columns of values are arithmetic sequences.

Start at the leftmost point and count the blocks up to the line of the next point.

Now count the blocks right to the next point.

Compare these to dy and dx.

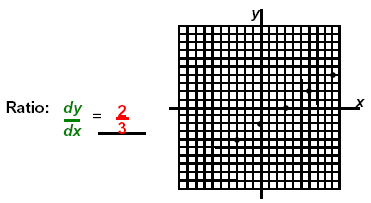
The following is another approach to graphing this equation.

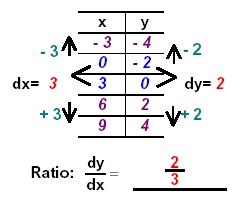
If both the x-intercept and the y-intercept are integers, we can place them in the middle of the table. Then we can find the difference in the x-values for dx and the difference in the y-values for dy and use these differences to build arithmetic sequences for the table.

Let x = 0, then 2( 0 ) − 3y = 6 or y = -2

which gives the point: ( 0 , -2 )

Let y = 0, then 2x − 3( 0 ) = 6 or x = 3

which gives the point: ( 3 , 0 )

Check the dy and dx on your table.

Now you must CHECK the top and bottom points in the table to be sure that they are points on the line:

For the point (- 3, - 4) replace x = - 3 and y = - 4 in the given equation 2x − 3y = 6

CHECK:

For the point (9, 4) replace x = 9 and y = 4 in the given equation 2x − 3y = 6

CHECK: