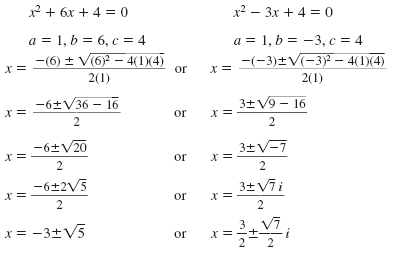Home
Power of a Power Property of Exponents
Adding and Subtracting Rational Numbers
Point
Solving Equations with Radicals and Exponents
Quadratic Equations
Using Intercepts for Graphing Linear Equations
Graphing Linear Equations in Two
Exponents
Multiplying Fractions
Solving Linear Equations Containing Fractions
Evaluating Polynomials
Multiplication Property of Square and Cube Roots
Writing a Fraction in Simplest Form
Square Roots
Inequalities
The Pythagorean Theorem
Factoring The Difference of 2 Squares
Solving Polynomial Equations
Roots and Powers
Writing Linear Equations in Standard Form
Solving Nonlinear Equations by Substitution
Straight Lines
The Square of a Binomial
Solving Equations
Adding and Subtracting Like Fractions
Point
Finding the Equation of an Inverse Function
Slope of a Line
Rules for Nonnegative Integral Exponents

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Nonlinear Equations by Substitution

Example

Solve for x:

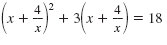
Solution		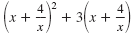= 18
Step 1 Write the equation in quadratic form.
Subtract 18 from both sides.		= 0
Step 2 Use an appropriate â€œuâ€ substitution. Substitute u for	u² + 3u - 18	= 0
Step 3 Solve the resulting equation. Factor the new equation. Use the Zero Product Property. Solve each equation for u.	(u + 6)(u - 3) u + 6 = 0 or u - 3 u = -6 or u	= 0 = 0 = 3
Step 4 Substitute the original expression for u.		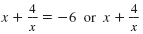= 3
Step 5 Solve for the original variable. Multiply both sides of each equation by x. Write each equation in standard form.	x² + 4 = -6x or x² + 4 x² + 6x + 4 = 0 or x² - 3x + 4	= 3x = 0

Neither equation factors. So, we will use the quadratic formula to solve each:

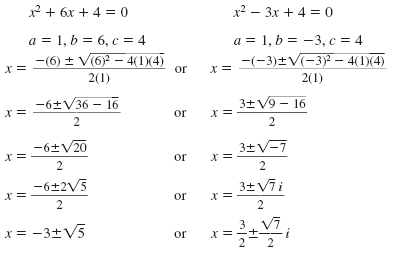
So, there are four solutions:

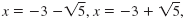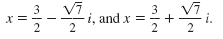
The equation 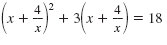written in standard form is

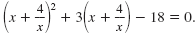
The graph of the corresponding function,

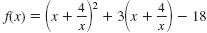is shown.

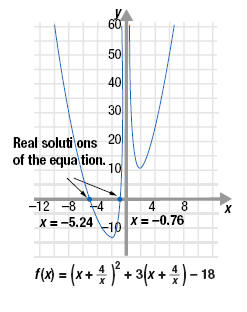
The graph crosses the x-axis at the two locations corresponding to the two real solutions of the equation:

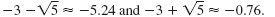
Note that x is in a denominator and so it cannot equal 0. Therefore, the line x = 0 is a vertical asymptote.