Point-slope Form for the Equation of a Line
Example 1
Find the equation of the line that passes through the point (-4, 7) with
slope
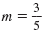 . .
Solution
| Use the point-slope formula.
|
y - y1 |
= m(x - x1) |
| We are given the point (-4, 7),
so let x1 = -4 and y1 = 7. |
y - 7 |
= m(x - (-4)) |
The slope is
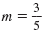 . . |
y - 7 |
 |
| Simplify the right side. |
y - 7 |
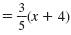 |
So, the equation of the line is
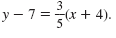 |
|
Example 2
Find the equation of the line that passes through the points (3, -3) and (6,
-1).
Solution
| First, find the slope of the line.
|
|
|
| Let (x1, y1) = (3, -3) and
(x2, y2) = (6, -1). |
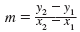 |
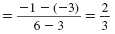 |
| Next, use the point-slope formula.
|
y - y1 |
= m(x - x1) |
| We can use either given point.
Let’s use (6, -1). |
y - (-1) |
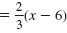 |
| Simplify the left side. |
y + 1 |
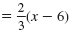 |
So, the equation of the line is
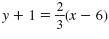 |
|
|
Note:
If we had used the other point, (3, -3), we would have obtained:
| y - y1 |
= m(x - x1) |
| y - (-3) |
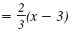 |
| y + 3 |
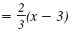 |
This equation is equivalent to
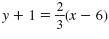 since both simplify to since both simplify to
 . .
|

