Square Roots

Definition — Square Root

For a nonnegative real number, a, the principal square root of a is written If b is a nonnegative real number and b² = a, then

Example:

because 7 is nonnegative and 7² = 49.

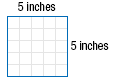
We can use geometry to provide a visual interpretation of a positive square root.

For example, suppose a square has an area of 25 square inches. The length of each side is the principal square root of the area. That is,

the length of a side of the square = = 5 inches.

A perfect square is a number that has a rational square root.

As we work with square roots, we will find it helpful to recognize perfect squares and their square roots. The table lists some whole number perfect squares and their principle square roots.

To approximate the square root of a number that is not a perfect square, we can estimate or use the key on a calculator.

Perfect Squares	Principal Square Roots
02 = 0
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100

Property — Squares and Square Roots

English Squaring and taking a square root “undo” each other.

Algebra If a is a nonnegative real number, then

Example