|
Home |
The Pythagorean TheoremObjective Learn how to use the Pythagorean Theorem to find the length of the side of a right triangle and to solve problems. The Pythagorean Theorem is probably the most famous theorem in mathematics. Its history dates back to about 2500 years ago to the famous Greek mathematician and philosopher Pythagoras. However, some historians think that the theorem dates back even further as ancient writings have been found that list “Pythagorean triples” or triples of whole numbers that can be the lengths of the sides of a right triangle.
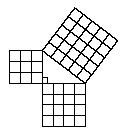
Modeling the Pythagorean TheoremLet's see a model for the Pythagorean Theorem.
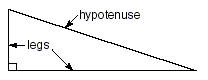
The sides of the right triangle have lengths of 3, 4, and 5 units, and the areas of the squares are 9, 16, and 25 square units, respectively. These numbers form the basis for the Pythagorean Theorem. The area of the larger square is equal to the total area of the two smaller squares. 5 2 = 3 2 + 4 2 25 = 9 + 16 This relationship is true for any right triangle. Before seeing the Pythagorean Theorem in its algebraic form, let's check the following: • The sides of a right triangle that are adjacent to the right angle are called the legs of the triangle. • The side opposite the right angle is called the hypotenuse.
The Pythagorean Theorem In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
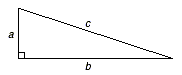
c 2 = a 2 + b 2
How are the model of the Pythagorean Theorem and the expression c 2 = a 2 + b 2 related? Suppose the lengths of the sides of the right triangle in the model are a, b, and c with c being the longest side. Then, the areas of the squares would be a 2, b 2, and c 2, respectively, and c 2 would equal the sum of a 2 and b 2. |